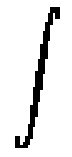Brain Image Warping and Pathology Detection

by

Paul Thompson

(continued from previous page...)

Model-Driven Algorithms

The extreme difficulty of matching brain data based on intensity criteria alone led to the development of algorithms driven by anatomical models, which can be extracted from each dataset prior to registration. Anatomic models provide an explicit geometry for individual structures in each scan. Model-driven algorithms can be classified by the type of features that drive them. These features include point, curve or surface models of anatomic structures. When parameterized consistently (see Section 3), mesh-based models of anatomic systems help guide the mapping of one brain to another. Anatomically-driven algorithms guarantee biological as well as computational validity, generating meaningful object-to-object correspondences, especially at the cortex.

Point-Based Matching. The simplest set of anatomic features which can guide the mapping of one brain to another is a set of point landmarks, identified manually (Bookstein, 1989) or automatically (Amit, 1997; Davis et al., 1997) in each dataset. A specification of correspondences at point landmarks can be extended to produce a deformation field for the full volume in a variety of ways, each consistent with the displacements assigned at the point landmarks. The ambiguity is resolved by requiring the deformation field to be the one that minimizes a specific regularizing functional (Tikhonov and Arsenin, 1977), which measures the roughness or irregularity of the deformation field, calculated from its spatial derivatives. Different regularizers measure smoothness in different ways, and correspond to different ways of interpolating the deformation from the points into the full 3D volume. All regularizers penalize large values of the derivatives, creating warping functions that take on the values to be interpolated (displacements) at the specified points, but which do not vary erratically elsewhere. For producing 2D warping fields, thin-plate splines (Grimson, 1981; Bookstein, 1989) are functions which minimize the penalty:

J_thin-plate(u) = 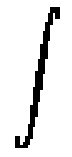_R2 [ (d₁₁u)² + 2(d₁₂u)² +(d₂₂u)² ] dx₁ dx₂

where d_iju is the partial derivative of u with respect to x_i and x_j.

Other members of the family of multidimensional spline functions (Duchon, 1975; Meinguet, 1979; Wahba, 1990) have also been used for brain image warping. Membrane splines (Amit et al., 1991; Gee et al., 1993) and elastic body splines (Miller et al., 1993; Davis et al., 1997) are warping functions which minimize the following measures of irregularity:

J_memb(u) = 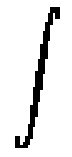_R2 [ (d₁u₁)² + (d₁u₂)² + (d₂u₁)² + (d₂u₂)² ] dx₁ dx₂

J_elas(u) = 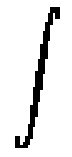_R2 _{i=1 to 2 j=1 to 2} [ (l/2)(d_iu_i)(d_ju_j) + (m/4)[(d_iu_j)(d_ju_i)]² ] dx₁ dx₂

where l and m are the elasticity coefficients.

Just like the continuum-mechanical warps defined earlier, the warping fields generated by splines satisfy partial differential equations of the form Lu(x)=-F(x), where u(x) is fixed at the specified points, F(x) plays the role of a body force term, and L is the biharmonic differential operator for the thin-plate spline, the Laplacian operator for the membrane spline, and the Cauchy-Navier operator for the elastic body spline (see Footnote 1).

Footnote 1: Note that spline-based warping functions can be defined either (1) as the variational minimizer of an irregularity measure or (2) as solutions to related PDEs. But, as pointed out by Arad (1995), strictly one looks for solutions to each problem in different function spaces (the Sobolev space H²(W) for minimizing the regularizing integral - which is also known as a Sobolev semi-norm - and continuous function spaces for solving PDEs).

Once a type of spline is chosen for warping, a formula can be used which specifies how to interpolate the displacement field from a set of points {x_i} to the surrounding 2D plane or 3D volume: u(x) = p_m-1(x) + _i c_i G(x-x_i)

Here p_m-1(x) is a polynomial of total degree m-1, where m is the order of derivative used in the regularizer, and G is a radial basis function or Green's function whose form depends on the type of spline being used (Joshi et al., 1995; Davis et al., 1997).

The polynomial coefficients determine components of low-order data variations, such as a global rigid motion between the two brains, which are not penalized by the smoothness functional (Wolberg, 1990). The coefficients c_i in this formula are found by evaluating this equation at the points x_i and solving the resulting linear system of equations. Various choices of radial basis functions G(r), for r=||(x-x_i)||, are commonly used for medical image matching, and for multivariate data interpolation generally (Bookstein, 1989; Ruprecht and Mueller, 1995; Thompson and Toga, 1996). Their behavior is also well-understood from their wide use in neural networks and pattern classifiers (Ripley, 1996). Choices of r²ln r and r correspond to the thin-plate spline in 2D and 3D,
with r³ for the 3D volume spline (Davis et al., 1997),
the 3x3 matrix [ar²I-3xx^T]r for the 3D elastic body spline (Davis et al., 1997), and

(r²+c²)^a (a in [0,1]) and ln(r²+c²)^1/2 (c in [0,1])

for multiquadric and shifted-log interpolants (Franke, 1979; Hardy, 1990; Ruprecht and Mueller, 1995).

Gaussian radial functions:

G(r)=exp(-r²/2s²)

belong to the same family, generating warping fields that minimize the following non-intuitive irregularity measure (Poggio and Girosi, 1990):

J_gauss(u) = _{n=0 to infinity} (-1)ⁿ(s²ⁿn!2ⁿ) i₁ to i_{n R}2 [ dⁿu(x) / (dx_i1...dx_in) ]² dx

These Gaussian functions perform poorly unless s is chosen carefully (Wolberg, 1990; Franke (1979) suggests using s=1.008d/n, where d is the diameter of the point set and n is the number of points). The best choice of radial basis functions depends on the application objectives. For modeling deformation of real biological tissue, elastic body splines out-perform thin-plate splines (Davis et al., 1997). Thin-plate splines, however, are advantageous in computing shape statistics (Bookstein, 1989). Use of radial basis functions in medical image registration algorithms has also been extended to neural network implementations (Davis et al., 1996).

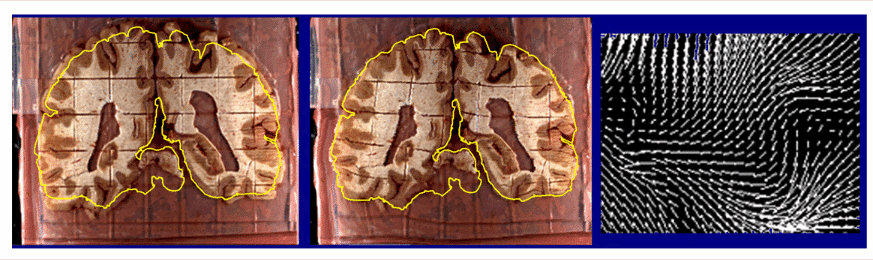
Curve-Based Approaches. When constructing a warping field for matching two brain images, greater anatomical accuracy can be achieved by using curves as anatomic driving features. In 2D, matching of planar curved boundaries is ideal for correcting deformations in histologic tissue (Schormann et al., 1996; Mega et al., 1997; see Fig. 1).

Fig. 1. Recovery of Change in Brain Tissue due to Post Mortem Effects and Histologic Processing. Warping algorithms based on continuum-mechanical models can recover and compensate for patterns of tissue change which occur in post mortem histologic experiments. A brain section (left), gridded to produce tissue elements for biochemical assays. is reconfigured (middle) into its original position in the cryosection blockface (Mega et al., 1997; algorithm from Thompson and Toga, 1996, 1998). The complexity of the required deformation vector field in a small tissue region (magnified vector map, right) demonstrates that very flexible, high-dimensional transformations are essential (Thompson and Toga, 1996; Schormann et al., 1996). As well as measuring local patterns of mechanical tissue deformations, recovery of deformation fields allows projection of histologic and biochemical data back into the volumetric reference space of the cryosection image. In some cases, these data can also be projected, using additional warping algorithms, onto in vivo MRI and co-registered PET data from the same subject for digital correlation and analysis (Mega et al., 1997).

Approaches using sulcal lines to drive a 3D volumetric warp are under active investigation in Macaque (Joshi et al., 1995) and human MR data (Declerck et al., 1995; Ge et al., 1995; Banerjee et al., 1995; Luo and Evans, 1995). Curve-based sulcal models can be combined with intensity-based measures to assist in matching cortical regions (Collins et al., 1996).

Declerck et al. (1995) use crest lines to drive a volume transformation. Crest lines (Monga and Benayoun, 1995) are curved loci on a surface which satisfy the following geometric criterion: the largest principal curvature must be locally maximal in the associated principal direction. After an MR dataset is thresholded to segment the cortex and ventricles, crest lines on these surfaces are defined. These automatically extracted features follow sulcal lines and gyral crests. They are matched with their counterparts in a target brain using (1) an iterative closest point algorithm, which finds candidate lines for matching, and (2) topological criteria to enforce one-to-one matching of curves and to ensure that their internal points are matched in a consistent, serial order. The 3D deformation field, expressed as a 3D tensor product of B-spline basis functions, is obtained by minimizing a regularizing term (as in point-based approaches) and a landmark mismatch term. This mismatch term limits the impact of spurious matches by tolerating some separation between curves which the algorithm decides to match.

Automated Matching. Identifying the subset of curved features which have a consistent topology across subjects (and are therefore appropriate to match) is extremely challenging. The problem is, however, easier than in the general intensity-matching case, as the parametric forms of the curves have a differentiable structure. The inherent structure in the model allows additional geometric features (torsion, curvature and local Frenet frames) to be included in the matching function, to favor correct pairing (Kishon et al., 1991; Gourdon and Ayache, 1993). Sulcal curvature patterns are only weakly conserved across subjects, and even this consistency is restricted to specific anatomic regions (Ono et al., 1990; Thompson and Toga, 1997). Nevertheless, to help guide the automated matching of curves and surfaces in anatomic data, statistical priors have been defined, for different types of sulci, to describe their expected curvature (Khaneja et al., 1998; Manceaux-Demiau et al., 1998), torsion (Gueziec and Ayache, 1994; Khaneja et al., 1998) and stereotaxic position (Thompson et al., 1996, 1997, 1998). In an alternative approach based on Markov Random Fields, Mangin et al. (1994) extract a 3D skeletonized representation of deep sulci, parse it into an attributed relational graph of connected surface elements. They then define a syntactic energy on the space of associations between the surface elements and anatomic labels, from which estimates of correct labelings (and therefore correct matches across subjects) can be derived.

Despite difficulties in pairing them automatically, crest lines provide a dense system of anatomic features to guide the volumetric mapping of one brain to another. Their variability and typical characteristics have also been investigated in a promising scheme for the automatic generation of multi-subject anatomical atlases (Subsol, 1995).

Surface-Based Approaches. Ultimately, accurate matching of brain data requires the individual matching of:

(1) entire systems of anatomic surface boundaries, both external and internal, and

(2) relevant curved and point landmarks, including ones within the surfaces being matched (e.g., primary sulci at the cortex, tissue type boundaries at the ventricular surface).

In our own model-driven warping algorithm (Thompson and Toga, 1996, 1997, 1998), systems of model surfaces are first extracted from each dataset, and used to guide the volumetric mapping of one brain to another. The model surfaces include many critical functional interfaces, as well as numerous cytoarchitectonic and lobar boundaries in 3 dimensions. Both the surfaces and the landmark curves within them are reconfigured and forced to match their counterparts in the target datasets exactly. We will discuss this approach in some detail.

Anatomical Models. Since much of the functional territory of the human cortex is buried in the cortical folds or sulci, a generic structure is built to model them (Fig. 2; Thompson and Toga, 1996), incorporating a priori topological and shape information about the deep sulcal pattern. The underlying data structure consists of a connected system of surface meshes, in which the individual meshes are parametric, and have the form of complex 3D sheets which divide and join at curved junctions to form a network of connected surfaces.

Fig. 2. Connected Surface Systems used to Drive the 3D warp.

Parameterization. Surface parameterization, or imposition of an identical regular structure on anatomic surfaces from different subjects (Fig. 3), provides an explicit geometry which can be exploited to drive and constrain the correspondence maps which associate anatomic points in different subjects.

Fig. 3. Parametric Mesh Construction.

Footnote 2. For example, the calcarine sulcus (see Fig. 2) is partitioned into two meshes (CALCa and CALCp) to ensure that the complex 3D curve forming their junction with the parieto-occipital sulcus is accurately mapped under both the surface displacement and 3D volumetric maps reconfiguring one anatomy into the shape of another. Fig. 4 illustrates this procedure, in a case where 3 surface meshes in one brain are matched with their counterparts in a target brain. A separate approach (discussed later, Section 3) is used to match systems of curves lying within a surface with their counterparts in a target brain.

Displacement Maps. For each surface mesh M_l^p in a pair of scans A_p and A_q we define a 3D displacement field:

W_l^pq[r_l^p(u,v)] = r_l^q(u,v)-r_l^p(u,v)

carrying each surface point r_l^p(u,v) in A_p into structural correspondence with r_l^q(u,v), the point in the target mesh parameterized by rectangular coordinates (u,v). This family of high-resolution transformations, applied to individual meshes in a connected system deep inside the brain, elastically transforms elements of the surface system in one 3D image to their counterparts in the target scan.

Fig. 4. Scheme for Matching Connected Systems of Anatomic Surfaces.

{1/d_l^p(x)}/ _{l= 1 to L}{1/d_l^p(x)}.

Then W^pq(x), the displacement vector which takes a general point x in scan A_p onto its counterpart in scan A_q, is given by the linear combination of functions:

W^pq(x) = g_l^p(x). D_l^pqnp_l^p(x)), for all x in A_p

Fig. 5. Volume Warp Calculation.

D_l^pqnp_l^p(x) = { _{r in B(x;rc)} w_l^p (x,d_l^p(r)).W_l^pq[np_l^p(r)] dr} / { _{r in B(x;rc)} w_l^p(x,d_l^p(r)) dr }.

W_l^pq[np_l^p(r) is the (average) displacement vector assigned by the surface displacement maps to the nearest point(s) np_l^p(r) to r on M_l^p. R_c is a constant, and B(x;r_c) is a sphere of radius r_c = min{R_c, min{d_l^p(r)}}.

The w_l^p are additional weight functions (Fig. 5(b)) defined as

w_l^p(x,d_l^p(r)) = exp(-{d(np_l^p(r),x)/d_l^p(x)}²),

where d(a,b) represents the 3D distance between two points a and b. The Jacobian of the transformation field at each point x is tracked during the computation, as recommended by Christensen et al. (1995). In rare cases where the transformation is locally singular, the vector field computation is discretized in time, and the deformation field is reparameterized at successive time-steps, as suggested in (Christensen et al., 1996). Intermediate surface blends (1-t)r_l^p(u,v)+tr_l^q(u,v), (t in [0,1]), are generated for every surface, and these surfaces are uniformly reparameterized at times 0 ..t_m .. t_m+1 .. 1.

The M warps mapping the full surface system and surrounding volume from one time-point to the next are concatenated to produce the final transformation. This incremental evolution of the transformation is visualized in a published video (Thompson and Toga, 1998). Recent extensions of the core algorithm to include continuum-mechanical, and other filter-based models of deformation (cf. Joshi, 1995; Davatzikos, 1996) have yielded similar encouraging results.

Experiments illustrating the performance of the algorithm on MRI and high-resolution cryosection data are shown in Figs. 6 and 7.

Fig. 6. Different Maps produced by Surface-Driven Warping, and Accuracy of Warping Approach. The resulting deformation maps can be analyzed with local differential operators to emphasize the shearing (top left) or magnitude (top right) of the mapping transformation. It is important that these algorithms match anatomic boundaries with proven accuracy (lower panels) before they can be used to monitor anatomical shape change.

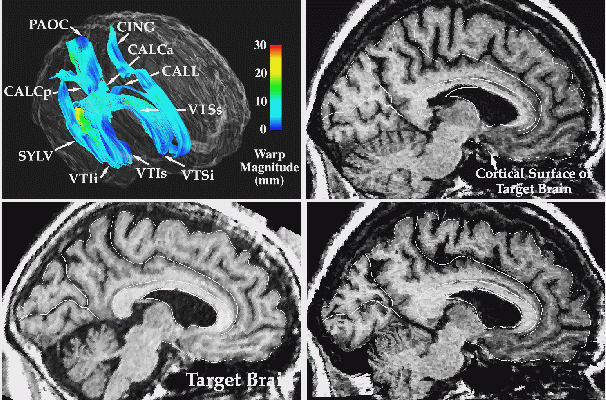
Fig. 7. Warping Measures Anatomical Change. Surface models are used to drive one brain into the configuration of the other. Here a warping algorithm driven by an extensive system of parametric surfaces (top left) is used to measure anatomic differences across subjects. You can see that when one brain (top right) is transformed to match the other (lower left), the entire anatomy of the cortex and deep anatomic surfaces are reconfigured (lower right) to match the target dataset.

Page 3 (continued on next page)

Related Publications